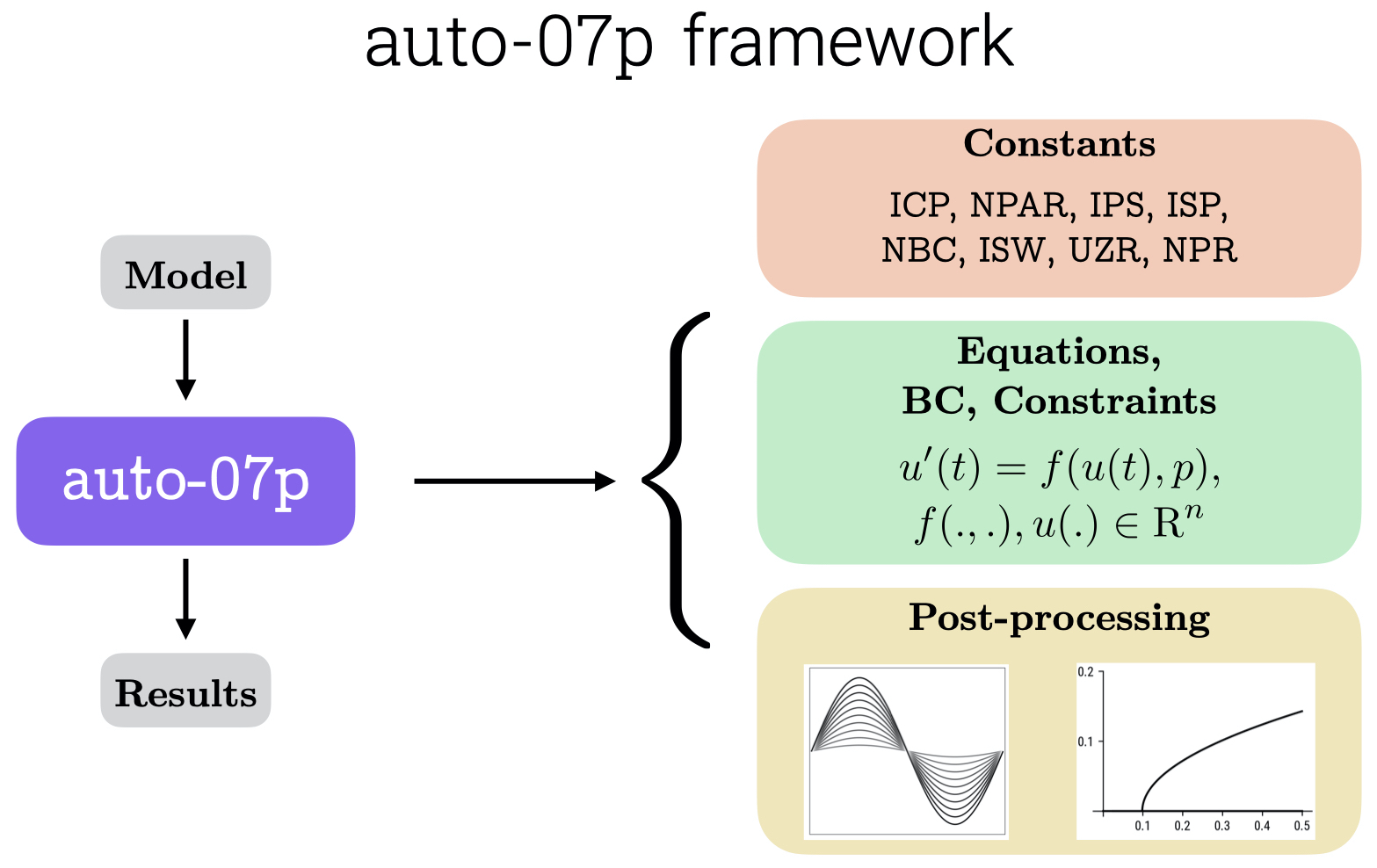
auto-07p framework

The framework that we use to solve elastic instability problems has 3 major steps.

1. To identify the model equations that describe the deformation field in elastic structure, derived either phenomenologically or from first principles. This is the part that captures the physics of the problem.

2. Using auto-07p to solve the system with the appropriate boundary conditions and continue the solution along a physical parameter in the system to see if the morphology changes with this parameter. auto-07p accepts first-order differential equations of the form u'(t) = f(u(t), p), \quad f(.,.), u(.) \in \text{R}^n, where p are the parameters in the problem.If we have a higher order system, we need to convert and represent it in this form. auto-07p finds solution to this equations i.e. f(u(t),p)=0 and will continue it along the different parameters p in the model. We will then look at the process of segregating the solution from the files that auto-07p spits out, post-processing them to understand the results.

3. Of course, the last step is to interpret the results and compare with experiments if any. And then go over to step (i) if there is mismatch between experiments and theoretical results.

The step I will be focusing in these tutorials is (ii) where we assume that the equations required to describe the elastic structure are already available. We will then extract the bifurcation diagram as well as plot the solution files.